Aichholzer et al. [AAAG95] presented an interpretation for the straight skeleton of simple polygons, which was extended to planar straight-line graphs by Aichholzer and Aurenhammer [AA96]. It turns out that this interpretation is a versatile tool in proofs of geometric properties of the straight skeleton. Further, it leads to one of the prominent applications of straight skeletons: roof construction and terrain modeling, see Section 1.3.2. The basic idea is to embed the wavefront propagation process in $R^3$ in the following sense: the first two dimensions represent the plane spatial dimensions and the third dimension reflects the temporal dimension. The wavefront propagation now defines the so-called terrain T (G) of $G$ as follows.

Aichholzer等人[AAAG95]提出了对简单多边形直线骨架的一种解释，Aichholzer和Aurenhammer [AA96]将其扩展到平面直线图。事实证明，这种解释是证明直线骨架几何性质的一种通用工具。此外，它引出了直线骨架的一个突出应用：屋顶建造和地形建模，见第1.3.2节。基本思想是将波前传播过程嵌入到$R^3$中，其含义如下：前两个维度表示平面空间维度，第三个维度反映时间维度。波前传播现在将$G$的地形定义为所谓的T (G)。

Definition 1.5 (terrain). The terrain T (G) of $G$ is defined by

定义 1.5 (地形)[NT0]。G 的地形 T (G) 定义为

$\mathcal {T}(G):=\bigcup _{t\geq 0}\mathcal {W}(G,t) \times \{t\}\tag{1.1}$

Figure 4 illustrates the terrain T (G) of the graph $G$ that is illustrated in Figure 3. Aichholzer et al. [AAAG95] used the term roof resp. island to indicate that T (P) of a simple polygon $P$ has the following two interpretations. Firstly, T (P) can be interpreted as a particular roof of a house for which $P$ models the footprint of the outer walls. Secondly, one can interpret $P$ as the coastline of an island that has the shape of T (P). If the surrounding sea floods the island then the rising coastline has the shape of the rising wavefront in $R^3$. In the case of planar straight-line graphs $G$ Aichholzer and Aurenhammer [AA96] use the term terrain for T (G).

图 4 说明了图 $G$ 的地形 T (G)，该图在图 3 中进行了说明。Aichholzer 等人 [AAAG95] 使用术语 roof resp.island 来表示简单多边形 $P$ 的 T (P) 具有以下两种解释。首先，T (P) 可以解释为房屋的特定屋顶，其中 $P$ 模拟了外墙的足迹。其次，可以将 $P$ 解释为具有 T (P) 形状的岛屿的海岸线。如果周围的海水淹没了该岛屿，那么上升的海岸线就具有 $R^3$ 中上升波前的形状。在平面直线图 $G$ 的情况下，Aichholzer 和 Aurenhammer [AA96] 使用术语 terrain 表示 T (G)。

The terrain T (G) consists of plane facets that have a slope identical to the inverse of the propagation speed of the wavefront edges, which is 1. An edge of T (G) can either be convex or reflex. In the ordinary sense, we call an edge $e$ of T (G) convex if the intersection of a small disk at any point in the relative interior of $e$ with the points below T (G) is always convex. A reflex edge $e$ of T (G) is defined likewise.

地形T(G)由平面组成，这些平面具有与波前边缘传播速度的倒数相同的坡度，即1。T(G)的边可以是凸边或凹边。通常意义上，如果位于$e$ 相对内部的任何一点上的小圆盘与T(G)下方点的交集始终是凸的，则我们称T(G)的边$e$ 为凸边。T(G)的凹边$e$的定义类似。

Definition 1.6 (reflex/convex arc, valley, ridge). We call the arcs of S (G) which are traced out by reflex (convex) wavefront vertices reflex arcs (convex arcs). We call a reflex edge of T (G) a valley and a convex edge of T (G) a ridge.

定义 1.6（凹/凸弧，谷，脊）[NT0]。我们称由凹（凸）波前顶点描绘出的S (G)的弧为凹弧（凸弧）。我们称T (G)的凹边为谷，T (G)的凸边为脊。

Observation 1.7 ([AAAG95, AA98]). The straight skeleton S (G) is the projection of the valleys and ridges of T (G) onto the plane $R2 × {0}$. Moreover, the valleys correspond to the reflex arcs and the ridges correspond to the convex arcs.

观察 1.7 ([AAAG95, AA98])[NT2].直线骨架 S (G) 是 T (G) 的谷和脊在平面 $R2 × {0}$ 上的投影。此外，谷对应于凹弧，脊对应于凸弧。

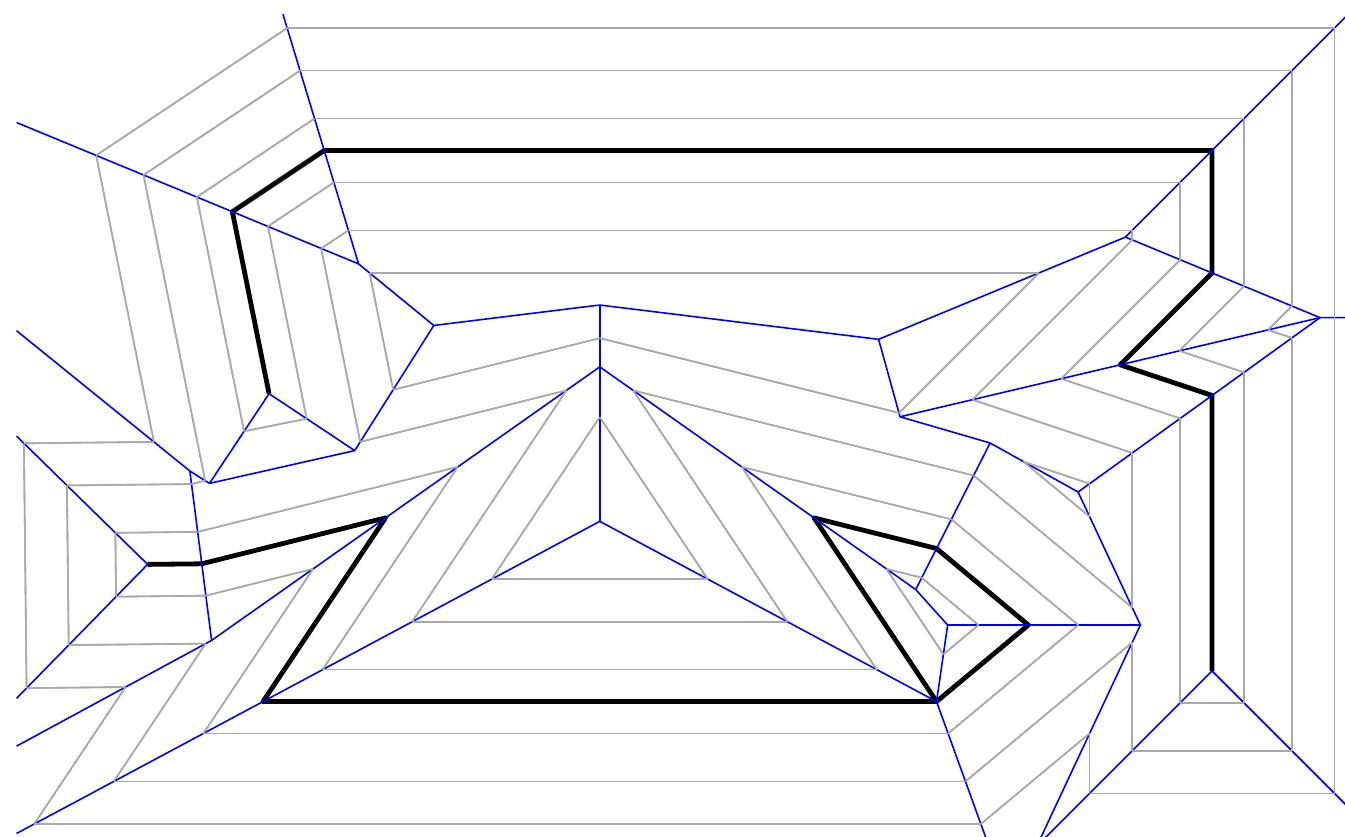
Figure 3: The straight skeleton S(G) (blue) of the planar straight-line graph $G$ (bold). The wavefronts at three points in time are depicted in gray.

图3：平面直线图$G$（粗体）的直骨架S(G)（蓝色）。以灰色描绘了三个时间点的波前。

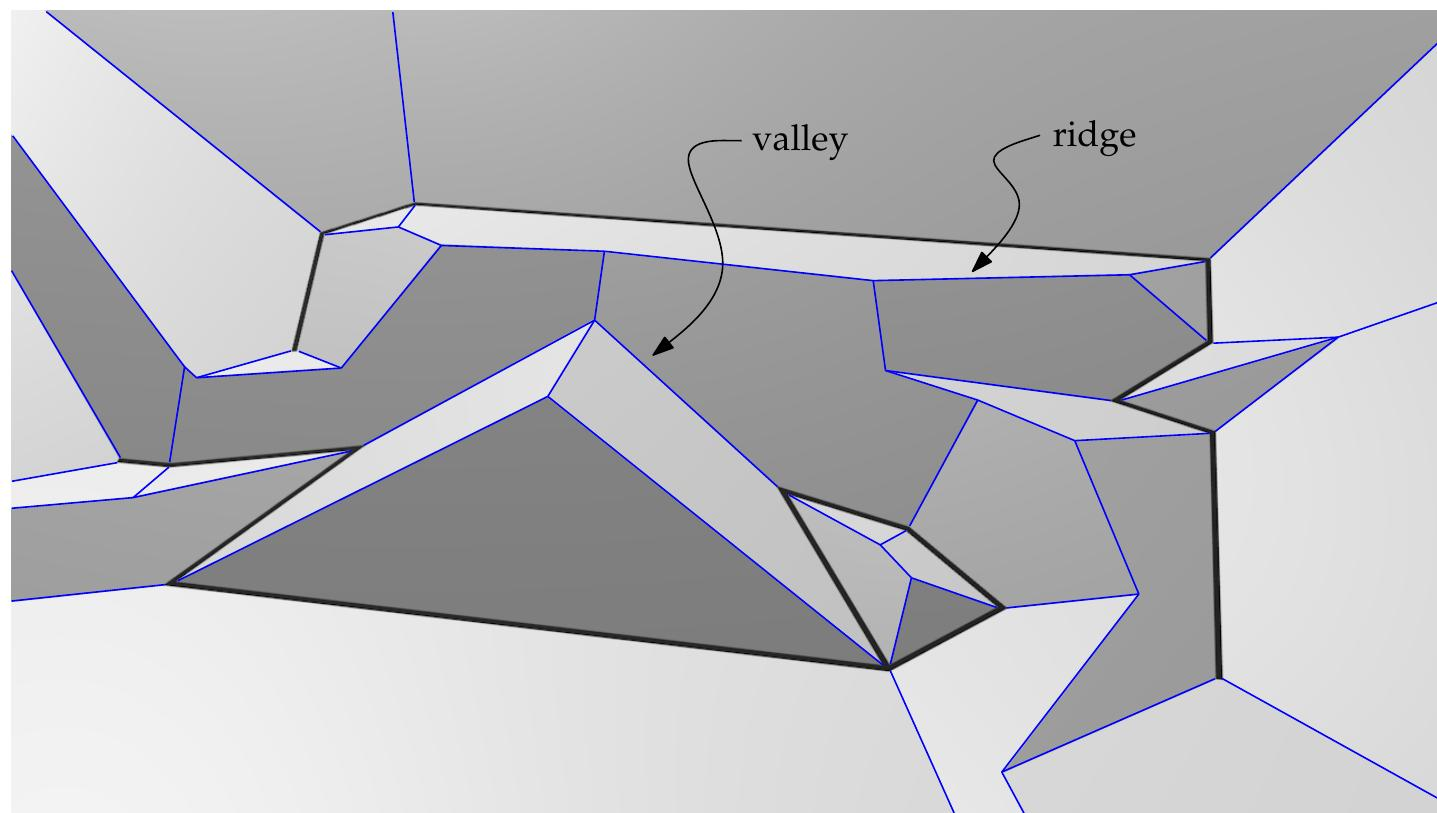
Figure 4: The terrain T (G) of the graph $G$ which is illustrated in Figure 3. The ridges and valleys are in blue. 图 4：图 $G$ 的地形 T (G)，如图 3 所示。山脊和山谷以蓝色表示。

roofs of polygons Aichholzer et al. [AAAG95] discussed the roof model of simple polygons $P$ in more detail. They investigated more general roofs $R$ on $P$ which fulfill the property that each facet lies on a plane that contains an edge of $P$ and has slope $1$. The question arises whether such an $R$ is equal to T (P). It turns out that this is not necessarily the case. However, $R$ and T (P) are equal if all valleys of $R$ are incident to $P$, or alternatively, if for any point x ∈ R the path of the steepest descent leads to $P$. In other words, Aichholzer et al. [AAAG95] showed that among all roofs, T (P) has the peculiar property that it does not accumulate water when it is raining.

Aichholzer等人[AAAG95]讨论了简单多边形$P$的屋顶模型的更多细节。他们研究了$P$上更一般的屋顶$R$，这些屋顶满足每个面都位于包含 P的边且斜率为$1$的平面上的性质。问题出现了，这样的$R$是否等于T(P)。事实证明，情况并非总是如此。然而，如果$R$的所有谷都与 $P$相关联，或者，如果对于任何点x ∈ R，最陡下降的路径通向$P$，则$R$和T(P)相等。换句话说，Aichholzer等人[AAAG95]表明，在所有屋顶中，T(P)具有一个独特的性质，即下雨时它不会积水。

Following the notation of Cheng and Vigneron [CV07], we denote by aˆ the edge of T (G) that corresponds to the arc a in S (G). Analogously, we denote by fˆ(e) the facet of T (G) which corresponds to the face f (e) of S (G).

沿用 Cheng 和 Vigneron [CV07] 的符号，我们用 aˆ 表示 T (G) 的边，它对应于 S (G) 中的弧 a。类似地，我们用 fˆ(e) 表示 T (G) 的面，它对应于 S (G) 的面 f (e)。