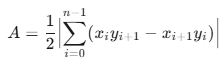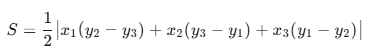```

  // 计算面积（使用鞋带公式）
  double area() const {
      if (size() < 3) return 0.0;
      
      double area = 0.0;
      int n = size();
      for (int i = 0; i < n; ++i) {
          int j = (i + 1) % n;
          area += at(i).x * at(j).y;
          area -= at(j).x * at(i).y;
      }
      return std::abs(area) / 2.0;
  }

```

鞋带公式（Shoelace Formula，又称高斯面积公式）用来求任意简单多边形（不自交）的面积，只要知道各顶点按顺序（顺/逆时针均可）的平面坐标即可。

1. 公式写法

设多边形有 n 个顶点

P₀(x₀,y₀), P₁(x₁,y₁), …, Pₙ₋₁(xₙ₋₁,yₙ₋₁)， 则面积

下标循环：i+1=n 时取 0。

把相邻顶点“交叉相乘”再相减，最后取绝对值除以 2，形状像“系鞋带”而得名。

2. 三角形特例

三点 A(x₁,y₁), B(x₂,y₂), C(x₃,y₃)