弹性力学基础教程:从三维到二维
本教程旨在梳理弹性力学的核心理论框架,对比三维空间与二维平面问题(平面应力与平面应变)的数学描述。
1. 基本变量 (Basic Variables)
在弹性力学中,我们需要求解物体内部的应力、应变和位移。
1.1 三维情形 (3D)
在三维直角坐标系 $(x, y, z)$ 中,共有 15个 未知函数:
- 位移分量 (3个): $u, v, w$ 分别对应 $x, y, z$ 方向的位移。
- 应变分量 (6个):
- 正应变: $\varepsilon_x, \varepsilon_y, \varepsilon_z$
- 切应变: $\gamma_{xy}, \gamma_{yz}, \gamma_{zx}$
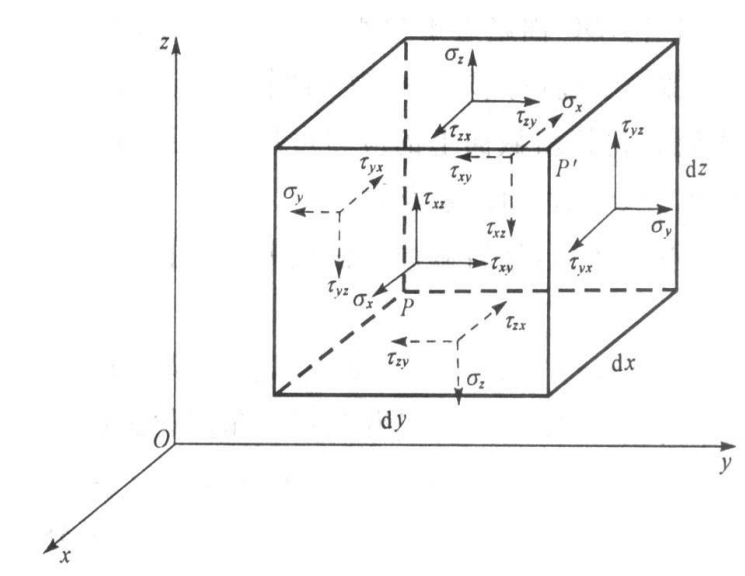
- 应力分量 (6个):
- 正应力: $\sigma_x, \sigma_y, \sigma_z$
- 切应力: $\tau_{xy}, \tau_{yz}, \tau_{zx}$ (注意对称性 $\tau_{xy}=\tau_{yx}$ 等)
1.2 二维情形 (2D)
二维问题通常简化为 $x-y$ 平面内的问题,变量减少至 8个:
- 位移分量 (2个): $u, v$
- 应变分量 (3个): $\varepsilon_x, \varepsilon_y, \gamma_{xy}$
- 应力分量 (3个): $\sigma_x, \sigma_y, \tau_{xy}$
2. 平衡方程 (Equilibrium Equations)
描述微元体在受力状态下的静态平衡关系。
2.1 三维平衡方程
$$ \begin{cases} \frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} + f_x = 0 \\ \frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \sigma_y}{\partial y} + \frac{\partial \tau_{zy}}{\partial z} + f_y = 0 \\ \frac{\partial \tau_{xz}}{\partial x} + \frac{\partial \tau_{yz}}{\partial y} + \frac{\partial \sigma_z}{\partial z} + f_z = 0 \end{cases} $$ 其中 $f_x, f_y, f_z$ 为单位体积的体力分量。
2.2 二维平衡方程
忽略 $z$ 方向的变化和分量: $$ \begin{cases} \frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + f_x = 0 \\ \frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \sigma_y}{\partial y} + f_y = 0 \end{cases} $$
3. 几何方程 (Geometric Equations)
描述应变与位移之间的微分关系(柯西方程)。
3.1 三维几何方程
$$ \begin{cases} \varepsilon_x = \frac{\partial u}{\partial x}, \quad \varepsilon_y = \frac{\partial v}{\partial y}, \quad \varepsilon_z = \frac{\partial w}{\partial z} \\ \gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \\ \gamma_{yz} = \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \\ \gamma_{zx} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \end{cases} $$
3.2 二维几何方程
$$ \begin{cases} \varepsilon_x = \frac{\partial u}{\partial x} \\ \varepsilon_y = \frac{\partial v}{\partial y} \\ \gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \end{cases} $$
4. 物理方程 (Physical Equations / Constitutive Laws)
描述应力与应变之间的关系(广义胡克定律)。假设材料为各向同性线弹性体。 $E$ 为弹性模量,$\nu$ (nu) 为泊松比,$G$ 为剪切模量 ($G = \frac{E}{2(1+\nu)}$)。
4.1 三维物理方程
应变表示应力形式: $$ \begin{cases} \varepsilon_x = \frac{1}{E}[\sigma_x - \nu(\sigma_y + \sigma_z)] \\ \varepsilon_y = \frac{1}{E}[\sigma_y - \nu(\sigma_x + \sigma_z)] \\ \varepsilon_z = \frac{1}{E}[\sigma_z - \nu(\sigma_x + \sigma_y)] \\ \gamma_{xy} = \frac{\tau_{xy}}{G}, \quad \gamma_{yz} = \frac{\tau_{yz}}{G}, \quad \gamma_{zx} = \frac{\tau_{zx}}{G} \end{cases} $$
4.2 二维物理方程
二维问题分为两种情况,物理方程有所不同。
4.2.1 平面应力 (Plane Stress)
适用于薄板问题($\sigma_z = 0, \tau_{xz}=0, \tau_{yz}=0$)。 $$ \begin{cases} \varepsilon_x = \frac{1}{E}(\sigma_x - \nu \sigma_y) \\ \varepsilon_y = \frac{1}{E}(\sigma_y - \nu \sigma_x) \\ \gamma_{xy} = \frac{\tau_{xy}}{G} = \frac{2(1+\nu)}{E}\tau_{xy} \end{cases} $$ 注:此时 $\varepsilon_z \neq 0$,$\varepsilon_z = -\frac{\nu}{E}(\sigma_x + \sigma_y)$
4.2.2 平面应变 (Plane Strain)
适用于长柱体问题($\varepsilon_z = 0, \gamma_{xz}=0, \gamma_{yz}=0$)。 $$ \begin{cases} \varepsilon_x = \frac{1-\nu^2}{E}(\sigma_x - \frac{\nu}{1-\nu}\sigma_y) \\ \varepsilon_y = \frac{1-\nu^2}{E}(\sigma_y - \frac{\nu}{1-\nu}\sigma_x) \\ \gamma_{xy} = \frac{\tau_{xy}}{G} \end{cases} $$ 注:此时 $\sigma_z \neq 0$,$\sigma_z = \nu(\sigma_x + \sigma_y)$
5. 外力边界条件 (Boundary Conditions)
描述物体边界表面 $S$ 上已知的外力 $\bar{T}$ 与内部应力的关系。 $l, m, n$ 为边界外法线的方向余弦。
5.1 三维边界条件
$$ \begin{cases} l\sigma_x + m\tau_{yx} + n\tau_{zx} = \bar{T}_x \\ l\tau_{xy} + m\sigma_y + n\tau_{zy} = \bar{T}_y \\ l\tau_{xz} + m\tau_{yz} + n\sigma_z = \bar{T}_z \end{cases} $$
5.2 二维边界条件
在二维平面曲线边界上,$n=0$ (这里的 $n$ 指 $z$ 方向余弦),$l = \cos(N, x), m = \cos(N, y)$。 $$ \begin{cases} l\sigma_x + m\tau_{yx} = \bar{T}_x \\ l\tau_{xy} + m\sigma_y = \bar{T}_y \end{cases} $$
总结对比表
| 概念 | 三维 (3D) | 二维 (2D) |
|---|---|---|
| 未知量数量 | 15个 (3位移, 6应变, 6应力) | 8个 (2位移, 3应变, 3应力) |
| 平衡方程 | 3个偏微分方程 | 2个偏微分方程 |
| 几何方程 | 6个方程 | 3个方程 |
| 物理方程 | 6个方程 | 3个方程 (需区分平面应力/应变) |
| 主要区别 | 包含 $z$ 方向所有分量 | 假设 $z$ 方向量为0或常数 |